[구글BERT의 정석] Chapter1: 트랜스포머 입문(2) (셀프 어텐션)
오늘은 저번 장에 이어서 셀프어텐션에 대해서 알아보겠습니다.
앞서 쿼리, 키 , 벨류 행렬을 어떻게 계산하는지와 해당 행렬들을 입력 행렬을 통해서 얻을 수 있다는 것을 확인했습니다

단어를 표현하기 위해서( 단어 간의 관계를 파악하기 위해서) 셀프 어텐션은 모든 단어를 연결하는 과정을 수행합니다.
이런 방법을 적용하는 이유는 문장의 모든 단어가 어떤 관게를 가지고 있는지 파악을 하면 학습에 도움이 되기 때문입니다.
이 셀프 어텐션은 총 4가지 단계로 이루어져 있습니다. 순서대로 살펴보겠습니다
1단계
첫번째로는 앞서 구했던 쿼리와 키 행렬을 내적 연산을 수행합니다

행렬의 내적(행렬 곱이라는 표현이 정확할 거 같습니다)은 행벡터와 열벡터의 내적과 동일합니다.
위의 그림의 예에서는 쿼리의 행벡터는 각각 I, am, a, boy를 나타내고
키의 열벡터 역시 동일한 순서로 각 단어를 의미합니다.
이에 따라서 결과적으로 나오는 행렬의 성분은 모든 단어 간의 내적과 동일합니다.
그렇다면 이게 무엇을 의미할까요?
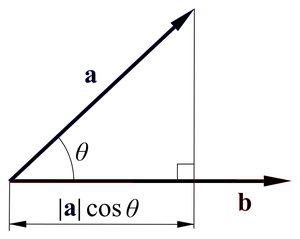
백터의 내적은 기하학적으로 봤을 때 사영이라고 얘기합니다. 좀 더 쉽게 얘기하면 a와 b를 내적시켰을 때
a가 b의 성분을 얼마나 가지고 있는지 다시 말하면 얼마나 유사한지에 따라서 그 크기가 결정됩니다.
즉 내적은 유사도를 의미한다고 볼 수 있습니다
여기서 다시 위의 쿼리,키의 내적으로 돌아가보겠습니다
결과로 나온 행렬은 모든 단어 간의 내적으로 이루어져 있습니다. 그리고 위에서 내적은 유사도라고 했습니다
그렇다면 우리가 1단계에서 구한 건 단어 간의 유사도라고 할 수 있겠습니다.
2단계
2단계에서는 . 키, 쿼리의 행렬 곱을 키 행렬의 차원의 제곱근으로 나누어 주겠습니다.
값을 줄여줌으로써, gradient 계산 시 안정적인 값을 얻을 수 있게 한다고 합니다.
3단계
지금까지 얻은 값은 정규화되어 있지 않은 상태입니다. 그렇기 때문에 대표적인 정규화 함수 Softmax를 통해
정규화 작업을 진행하겠습니다.
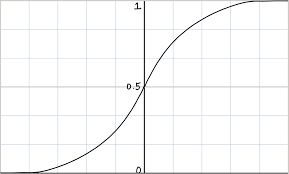
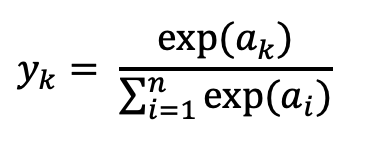
소프트맥스 함수는 0과 1사이의 값을 가집니다. 그렇기 때문에 2단계 값을 소프트맥스 함수에 넣어주면
각 행의 합이 1이 되는 행렬을 얻을 수 있게 됩니다.
이 행렬을 스코어(score)행렬이라고 하며, 각 단어가 몇%의 유사도를 가지는지를 의미합니다
4단계
지금까지 키, 쿼리의 내적을 수행하고 이를 차원의 제곱근으로 나누어주었으며, 소프트맥스로 정규화를 시켜주었습니다.
마지막으로는 어텐션(Z) 행렬을 계산하겠습니다.
지금까지 구했던 스코어 행렬에 밸류 행렬을 곱해주겠습니다.
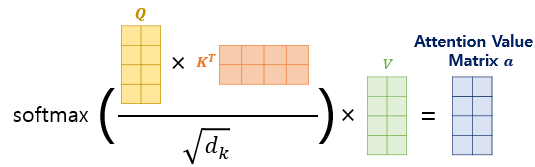
이렇게 구해준 어텐션 행렬은 밸류의 행백터 (위의 예시를 그대로 가져와 입력받은 문장은 I am good으로 그대로 사용하겠습니다) v1(I), v2(am), v3(good)으로표시가 됩니다.
Z의 행벡터 Z1을 예로 들면, Z1= 0.21v1 + 0.03v2+0.76v3의 꼴로 주어집니다.
요악하면,
1. 쿼리와 키의 내적 연산
2.키 행렬의 차원의 제곱근으로 나눠줌(스코어 행렬)
3.소프트맥스를 통한 정규화
4.스코어와 밸류의 곱(어텐션 행렬)
셀프 어텐션은 내적을 2의 과정으로 나누어주기 때문에, scaled dot product라고도 부릅니다.
여기까지 셀프 어텐션에 대해 알아보았습니다.
다음 시간에는 멀티 헤드 어텐션에 대해 알아보겠습니다