Algorithm

[알고리즘]이진 탐색(binary search) 알고리즘(+python구현)

Im_light.J 2023. 2. 4. 05:00
728x90

코딩 테스트 문제를 풀다보면, 배열에서 내가 원하는 원소가 들어 있는지 확인 해야하는 일이 꽤 있습니다

 

if a in arr: 
    print True

 

물론 파이썬에서는 이런 식으로 in, not in 연산을 통해 확인할 수 있습니다.

그런데 코딩테스트 문제에서는 시간 복잡도라는 걸 반드시 고려해야합니다 

 

배열에 대해서 몇번 정도만 원소를 탐색한다면 괜찮겠지만 모든 원소에 대해서 위치를 탐색하는 경우라면 어떨까요?

N의 길이를 가지면 배열에서 원소를 탐색하면 평균적으로 N/2정도만 뒤져보면 원소의 위치를 탐색할 수 있습니다

그러면 $N*N/2$ = > 시간복잡도 $O(N)$은 $ N^2$이 나오게 되는 상황이 나옵니다. 

 

배열의 길이가 짧은 경우는 상관이 없지만, 대부분 굉장히 긴 배열을 채점 단계에서 집어 넣어보는데 

$N^2$의 시간복잡도를 가지는 경우 시간 초과가 나올 확률이높습니다. 

 

 

그렇기 때문에 좀 더 효율적으로 탐색을 할 알고리즘이 필요합니다  

 

 

이진탐색의 개념은 간단합니다. 

 

1. 정렬된 배열   2.대소 비교 후 반으로 자른다 

 

이진 탐색을 수행하기 위해서는 배열이 순서대로 정렬되어 있어야 합니다. 

차순은 관계가 없지만, 여기서는 오름차순을 기준으로 설명드리겠습니다. 

 

 

그리고 위치를 알고싶은(혹은 존재 여부를 확인하고 싶은) 목표(target)를 배열의 중간값과 대소 비교를 수행합니다.  

그럼 세가지 경우가 존재하겠습니다 

 

1. 목표와 중간값이 같은 경우 

 

이 경우 탐색을 멈추고, 구하는 값이 위치라면 인덱스를 return 하면 됩니다 

 

2. 목표가 중간값보다 큰 경우 

 

이 경우 배열은 오름차순으로 정렬되어 있기 때문에 중간값을 기준으로 작거나 같은 곳에는 원하는 목표가 

없는것이 확실할겁니다. 그렇기 때문에 아래쪽은 탐색할 필요가 없습니다. 

 

3.목표가 중간값보다 작은 경우 

 

이 경우는 2번과 반대의 경우입니다. 뒷 쪽을 탐색할 필요가 없는 상황입니다. 

단계별로 탐색해야하는 데이터가 절반씩 줄어들기 때문에 시간복잡도는 $O(logN)$을 가지게 됩니다. 

 

 

다음으로는 코드 구현을 보겠습니다. 

 

위에서 설명의 편의상 배열을 잘라 작은 배열로 만드는 것처럼 표현을 했습니다.

실제로는 위 그림과 같이 배열 자체를 자르진 않을겁니다. 값의 존재 유무를 탐색할 때는 상관 없지만 

인덱스를 구하는 상황에서는 배열을 자르면 인덱스 값이 바뀌기 때문입니다.

 

대신 배열에서 사용할 부분의 위치를 기억해두고 이를 업데이트 해주는 방식으로 진행하겠습니다. 

def binary_search(arr, target, start, end):
    
    mid = (start+end)//2 #대소 비교를 진행할 중간값
    if start == end : 
        return 0 
    else: 
        if arr[mid]==target:

            return mid  #중간값이 타겟과 같으면 return 
        elif arr[mid]>target: 

            return binary_search(arr,target,start, mid-1)
        #타겟이 중간값보다 작은 경우 더 뒤쪽에 있는 배열은 사용하지 않기 때문에 
        end를 mid보다 작은 부분까지만 사용하는 것으로 업데이트를 진행해줍니다 
        elif arr[mid]<target: 

            return binary_search(arr,target, mid+1, end)
        #위의 경우와 반대로 앞쪽의 배열은 사용하지 않습니다

 

재귀함수를 통해 단순하게 짜봤습니다. 

 

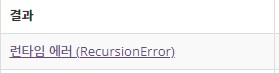
그런데 이런 방식으로 코드를 구현하면 이런 에러 문구를 만나기 정말 좋습니다 

백준에서 정해놓은 재귀의 깊이 보다 제가 구현한 코드가 더 깊어지는 경우인데, 

재귀함수의 경우 되도록 알고리즘 문제에서는 지향하는게 좋습니다 

 

 

def binary_search(arr, target, start, end):
    
        while start< end: 
            mid = (start+end)//2 
            if arr[mid]==target:
                return 1 
            elif arr[mid]>target: 
                end = mid- 1

            elif arr[mid]<target: 
                start =mid+ 1 
        return 0

반복문을 통해 동일하게 짜보았습니다 

 

728x90